Se zájmem jsem si přečetl diskuzi o problémech s LSB, neklidné dolní bity AD převodníku.
Ať už je to způsobené šumem nebo nepřesným převodníkem, tak při zobrazení na displeji to působí hodně rušivě. Z vlastní zkušenosti vím, že nepomůže ani průměrování, ani změna rozlišení AD převodníku. To může problém jenom snížit ale ne odstranit. I když bude měřené napětí stabilní, bez šumu ale zrovna na hraně mezi dvěmi digitálními hodnotami, tak se prostě budou střídat. A s jakou četností, to záleží na mnoha faktorech.
Ve svých konstrukcích se mi osvědčil vlastní způsob řešení tohoto problému.
Po každém AD převodu porovnám novou hodnotu se starou hodnotou.
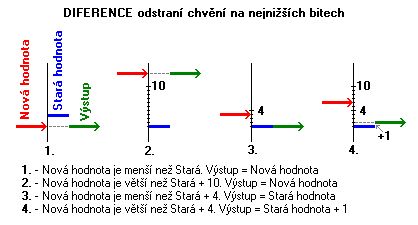
Při porovnávání mohou nastat 4 situace.
- Nová hodnota je menší než stará. Výstup bude nová hodnota.
- Nová hodnota je větší než stará + 10. Výstup je opět nová hodnota.
- Nová hodnota je menší nebo stejná jako stará hodnota + 4. Výstup se nemění, zůstává jako stará hodnota.
- Nová hodnota je větší než stará + 4. Výstup je stará hodnota + 1.
Hodnoty 10 a 4 jsou zvolené po dlouhodobém testování.
Pokud bude nová hodnota menší než stará, výstup je rovnou nová hodnota.
Při prudkém nárůstu (větší než 10) se vezme také nová hodnota.
Při nepatrné změně (do 4) se nic neděje, výstup zůstává stará hodnota. To právě odfiltruje nežádoucí šum (chvění).
A vtip této metody spočívá v tom, že při změně hodnoty v rozmezí 5 až 10 bude výstupní hodnota jenom o 1 větší než stará hodnota. Pokud se bude nová hodnota pomalu zvětšovat, bude výstup pěkně přičítat po jedné.
Nevýhodou tohoto řešení je zmenšení přesnosti. Výsledek převodu může být až o 4 menší než skutečnost.
Tento způsob se dá použít nejen pro AD převodníky ale i pro čtení dat z různých čidel a snímačů.
V assembleru pro PIC to vypadá takto:
;Diference, odstraní chvění na nejnižších bitech.
;VSTUP: A1,2=nová hodnota, B1,2=stará hodnota
;VYSTUP: B1,2=výsledek
;dál se používá C1,2 (x1=LOW byte, x2=HIGH byte)
DIF
;A1,2 - B1,2 = C1,2
MOVF B1,W
SUBWF A1,W ;A1-B1=W
MOVWF C1 ;uložit
MOVF B2,W
BTFSS STATUS,C ;odečet byl kladný?
ADDLW 1 ;NE, B2+1=W
SUBWF A2,W ;A2-B2=W
MOVWF C2 ;uložit
;C2 = nenulové? (A<B nebo A>B+255)
MOVF C2,F
BTFSS STATUS,Z ;C2=0?
GOTO ADB ;NE, nová hodnota z A
;C1 > 10? (A>B+10)
MOVF C1,W
SUBLW 10 ;10-C1
BTFSS STATUS,C ;kladné?
GOTO ADB ;NE, nová hodnota z A
;C1 <= 4? (A<=B+4)
MOVF C1,W
SUBLW 4 ;4-C1
BTFSC STATUS,C ;záporné?
RETURN ;NE, stará hodnota
;C1 > 4 (A>B+4)
INCFSZ B1,F ;stará hodnota B+1
RETURN ;
INCF B2,F ;
RETURN
ADB
MOVF A1,W ;přesun nové hodnoty A do staré B
MOVWF B1 ;
MOVF A2,W ;
MOVWF B2 ;
RETURN